Pattern Recognition Techniques
Applied to the Thyroid Gland Data
Kun Zhang
1. Introduction and Problem Formulation
2. Conventional solutions to the
problem
3. Self-Organizing Mapping (SOM)
4. Dimensionality Reduction (KL
Transformation)
5. Experimental Results
6. Conclusions
Reference
1. Introduction and Problem Formulation
An important scientific activity is to collect the results
of measurements. In the area of medicine, modern physical measuring methods
provide an ever increasing amount of information. For example, clinical
examination and complementary investigation, such as biochemical analyses,
result in a large possible a picture of the physiological (normal or abnormal)
status of a patient. Because of the availability of modern computer data-acquisition
methods, the assembling and storing of data has become more and more necessary,
and proper target-interpretation of these data has received more and more
attention resulting in a better utilization of the available information.
Pattern recognition is a mathematical discipline that
tries to extract and utilize information from a large amount of real or
complex data. In pattern recognition, measurements on samples, objects,
phenomena, etc. are used for a classification purpose on an objective and
formal basis. In medicine, the purpose of pattern recognition is the fitting
of patients into a well defined class [1].
Recall that comparison of many classification methods
based on a set of thyroid gland data which consists of 5 laboratory tests
relating to the thyroid function, has been done by Dr. Coomans in [2].
The data were collected for 215 patients divided in 3 classes, including
euthyroidism (normal), hypothyroidism and hyperthyroidism. In that study
18 discrimination techniques were compared on the basis of correct classification
rates, probability performance criteria and reliability. These techniques
included k-nearest neighbor classification, linear learning machine, Bayesian
classification on the basis of normal distributions and equal variance
for the training classes, and many more. Some results have been observed
from the comparison of correct classification rates for the different classifications.
First, in the normal/hypo differentiation the probabilistic k-NN method
performs less well than the non-probabilistic alternatives 1-NN and k-NN.
Second, although the simple histogram method – Bayesian classification
on the basis of frequency histograms is considered as primitive compared
to the other techniques, it behaves very well in the study. Finally, the
poor performance of some techniques may be due to the fact that in the
normal/hypo differentiation some of the laboratory tests are redundant,
which is not the case for the normal/hyper differentiation.
In this work, the thyroid gland functional data is used
to test different pattern recognition methods. The thyroid data are collected
from three classes. Let 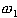 ,
, 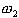 ,
and
,
and 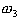 denote
the class of normal thyroid function, hyper-thyroid function, and hyperthyroid
function, respectively. An unknown pattern in each class is represented
by a feature vector
denote
the class of normal thyroid function, hyper-thyroid function, and hyperthyroid
function, respectively. An unknown pattern in each class is represented
by a feature vector 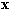 ,
where
,
where 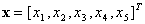 . First,
conventional classifiers are applied to the data without dimensionality
reduction, including Bayes method, Linear classifiers, and 1-NN. A kind
of neural network, Kohonen Self-Organizing Mapping (SOM) [3, 4], is also
used to the original data. Second, we use KL transformation to reduce the
dimension of the sampled data, then input the transformed data to the four
classifiers used previously, including the SOM neural network. In this
problem, since some information is lost after KL transform, the misclassification
rates increase in the low dimension case.
. First,
conventional classifiers are applied to the data without dimensionality
reduction, including Bayes method, Linear classifiers, and 1-NN. A kind
of neural network, Kohonen Self-Organizing Mapping (SOM) [3, 4], is also
used to the original data. Second, we use KL transformation to reduce the
dimension of the sampled data, then input the transformed data to the four
classifiers used previously, including the SOM neural network. In this
problem, since some information is lost after KL transform, the misclassification
rates increase in the low dimension case.
The remainder of this paper is organized as follows. In
section 2, we overview some conventional methods to the classification
problem. In section 3, the neural network - SOM is introduced to the problem.
We discuss in detail the architecture of the SOM system, the procedure
of SOM, and the method of selecting some critical parameters of SOM. The
KL transformation method is presented in section 4. We give the numerical
results of conventional methods and SOM in section 5. In section 6, we
summarize the work and give our conclusions.
[Return to Index]
2. Conventional solutions to the
problem
Some popular classifiers are considered in this section.
Since it is a problem in the three-class case, we discuss below the multi-class
version of each kind of classifier [5].
2.1 Bayes Classifier
Bayes decision theory is a fundamental statistical approach
to the problem of pattern recognition. This approach is based on the assumption
that the decision problem is posed in probabilistic terms, and that all
the relevant probability values are known.
Let us focus on the three-class case. The first assumption
of Bayes classifier is that the a priori probabilities 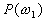 ,
, 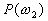 ,
and
,
and 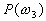 are
known. In practice, they can easily be estimated from the available training
feature vectors. Let
are
known. In practice, they can easily be estimated from the available training
feature vectors. Let 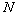 denote
the total number of available training patterns, and
denote
the total number of available training patterns, and 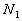 ,
, 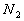 ,
and
,
and  of
them belong to class
of
them belong to class 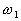 ,
, 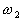 ,
and
,
and 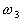 , respectively,
then
, respectively,
then 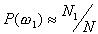 ,
, 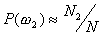 ,
and
,
and 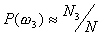 . The
other statistical quantities assumed to be known are the class-conditional
probability density functions
. The
other statistical quantities assumed to be known are the class-conditional
probability density functions  ,
describing the distribution of the feature vectors in each class. If we
assume that
,
describing the distribution of the feature vectors in each class. If we
assume that 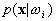 follow the general multivariate normal density, the problem of estimating
follow the general multivariate normal density, the problem of estimating 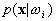 is reduced into that of estimating the mean value and the covariance matrix
of the
is reduced into that of estimating the mean value and the covariance matrix
of the 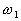 class,
as we will discuss later. Recall that the Bayes rule can be described as
class,
as we will discuss later. Recall that the Bayes rule can be described as
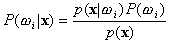 ,
,
where 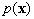 is the probable density function of
is the probable density function of 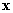 .
Then the Bayes classifier can now be stated as
.
Then the Bayes classifier can now be stated as
If  and
and 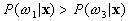 ,
, 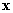 belong to
belong to 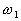 ,
,
If 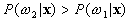 and
and 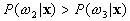 ,
, 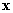 belong to
belong to 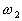 ,
,
If 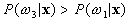 and
and 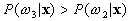 ,
, 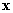 belong to
belong to 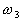 .
.
For the thyroid gland data, a Bayes classifier is designed
with assumption that all the data in each of the classes are generated
from the normal distribution. Now, the class-conditional probability density
functions of the 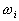 class
in the 5-dimensional feature space can be written as
class
in the 5-dimensional feature space can be written as
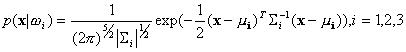 ,
,
where 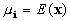 is the mean of the
is the mean of the 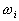 class and
class and 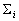 denotes the 5-by-5 covariance matrix defined as
denotes the 5-by-5 covariance matrix defined as
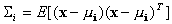 .
.
Let us define the discriminant functions, which involve
the logarithmic function:
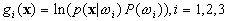 .
.
After removing the constant part of 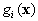 ,
we obtain the new discriminant function which represents a quadratic surface:
,
we obtain the new discriminant function which represents a quadratic surface:
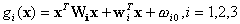 ,
,
where
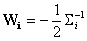 ,
,
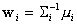 ,
,
and
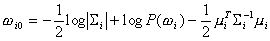 .
.
Bayes classifier can now be designed by using the discriminant
function as:
If 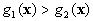 and
and  ,
, 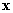 belong to
belong to 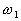 ,
,
If 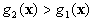 and
and  ,
, 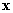 belong to
belong to 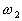 ,
,
If 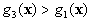 and
and  ,
, 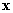 belong to
belong to 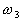 .
.
2.2 Linear Classifier
Linear classifier is another kind of widely used classifier,
since in some cases, the resulting classifiers are equivalent to a set
of linear discriminant functions. For example, a Bayes classifier with
assumption of equal covariance matrix for each of the classes. In this
section, we will design the optimal linear classifiers by adopting some
appropriate optimality criterions.
Let us consider the thyroid data in the three-class case.
Then our task is to devise three decision hyper-planes in the 5-dimensional
feature space, each of which can be given by:
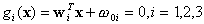 ,
,
where 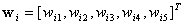 is known as the weight vector and
is known as the weight vector and 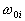 as the threshold.
as the threshold.
2.2.1 Fisher Criterion
It is well know that in the one-dimensional, two-class
problem Fisher criterion for the linear classifier is the optimal one.
But it doesn't work for more than two classes. Because we discuss the 3-class
case, we extend the Fisher Criterion to the multi-class case. In fact,
when the number of classes is larger than 2, the criterion is called the
trace optimization procedure.
Let
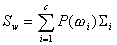 ,
,
 ,
,
where  denotes the number of classes,
denotes the number of classes, 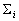 and
and 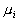 are
the covariance matrix and the mean value of the
are
the covariance matrix and the mean value of the 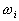 class, and
class, and 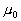 is the mean of all the data. Then the criterion can be expressed as:
is the mean of all the data. Then the criterion can be expressed as:
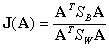 ,
,
where A is a matrix. Let
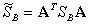 ,
,
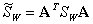 .
.
Then we calculate the eigenvectors of 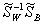 corresponding to the non-zero eigenvalues. Each eigenvector will be the
column of A. After the procedures above, the dimensionality of the input
data is reduced automatically down to the 2-dimensions for the 3 classes.
We then keep only the first feature. Thus, all the data are projected into
one dimension along the orientation of the left feature. By searching in
this direction, we can obtain two thresholds to optimally classify three
classes in one dimension.
corresponding to the non-zero eigenvalues. Each eigenvector will be the
column of A. After the procedures above, the dimensionality of the input
data is reduced automatically down to the 2-dimensions for the 3 classes.
We then keep only the first feature. Thus, all the data are projected into
one dimension along the orientation of the left feature. By searching in
this direction, we can obtain two thresholds to optimally classify three
classes in one dimension.
2.2.2 Bayes method with assumption of equal covariance
matrix for each class
As mentioned before, if we assume equal covariance matrices
for each class, we also can design a linear classifier by the Bayes rule.
Similar to the Bayes classifier, let
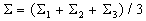 ,
,
and
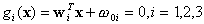
where  .
The decision rule is the same as that of the Bayes classifier discussed
previously.
.
The decision rule is the same as that of the Bayes classifier discussed
previously.
2.3 1-NN Classifier (leave-one-out)
The k-NN density estimation technique belongs to the nonparametric
method of pattern classification. Although it doesn't fall in the Bayesian
framework, it results in a suboptimal in practice. The algorithm for the
nearest neighbor can be summarized as follows. Given an unknown feature
vector 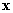 and
a distance measure, then:
and
a distance measure, then:
-
Out of the N training vectors, identify the k nearest neighbors,
k is chosen to be odd.
-
Out of these k samples, identify the number of vectors,
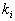 ,
that belong to class
,
that belong to class 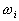 .
.
-
Assign
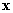 to the class
to the class 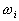 with
the maximum number
with
the maximum number 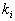 of samples.
of samples.
Various distance measures can be used, such as the Euclidean
and Mahalanobis distance. For the thyroid data, the simple version of this
algorithm, 1-NN rule, is used, because of the limited sample data. In other
words, a feature vector is assigned to the class of its nearest neighbor.
It is known that the classification error of the 1-NN
with the resubstitution procedure is always zero. Because the nearest neighbor
of a feature vector is always itself. So, we choose an alternative method
of 1-NN, which is known as the leave-one-out method. This method alleviates
the lack of independence between the training and test set in the resubstitution
method. The training is performed using N-1 samples, and the test is carried
out using the excluded sample. If this is misclassified an error is counted.
This is repeated N times, each time excluding a different sample.
[Return to Index]
3. Self-Organizing Mapping (SOM)
Self-Organizing Mapping is a kind of neural network, the
idea of which comes from the research of the functions of the human brains.
The SOM algorithm was presented in 1985 by Dr. Kohonen. In his book [3],
he states that a property which is commonplace in the brain but which has
always been ignored in the learning machines is a meaningful order of their
processing units. "Ordering " usually does not mean moving of units to
new places. The units may even by structurally identical; the specialized
role is determined by their internal parameters which are made to change
in certain processes. It then appears as if specific units having a meaningful
organization were produced.
Although a part of such ordering in the brain were determined
genetically, it will be intriguing to learn that an almost optimal spatial
order, in relation to signal statistics, can completely be determined in
simple self-organizing processes under the control of received information.
It seems that such a spatial order is necessary for an effective representation
of information in the internal models. The various maps formed in self-organization
are able to describe topological relations of input signals, using a one-
or two-dimensional medium for representation. Such dimensionality-reducing
mappings seem to be fundamental operations in the formation of abstractions.
From another point of view, the SOM algorithm belongs
to the class of competitive learning schemes (CLS). These schemes employ
a set of representatives 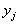 .
Their goal is to move each of them to regions of the vector space that
are dense in vectors of the input data. It must be emphasized that competitive
learning algorithm do not necessarily stem from the optimization of a cost
function.
.
Their goal is to move each of them to regions of the vector space that
are dense in vectors of the input data. It must be emphasized that competitive
learning algorithm do not necessarily stem from the optimization of a cost
function.
The general idea of the SOM algorithm is very simple.
When a vector x is presented to the algorithm, all representatives
compete with each other. The winner of this competition is the representatives 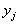 that lies closer to x according to some distance measure.
Then the winner is updated so as to move toward x, while
the losers either remain unchanged or are updated toward x
but at a much slower rate.
that lies closer to x according to some distance measure.
Then the winner is updated so as to move toward x, while
the losers either remain unchanged or are updated toward x
but at a much slower rate.
3.1 SOM algorithm
To introduce the basic self-organizing process, we use
the following array of the figure 3.1 for illustration.

Figure 3.1: Two-dimensional
self-organizing system
Consider the thyroid gland data. Let each unit receive the
same scalar signals 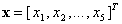 ,
then the output of the representative j can be written as:
,
then the output of the representative j can be written as:
 ,
,
where 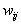 are the adaptive weights. In fact, every ordered set
are the adaptive weights. In fact, every ordered set 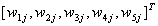 may
be regarded as a kind of image that shall be matched or compared against
a corresponding ordered set
may
be regarded as a kind of image that shall be matched or compared against
a corresponding ordered set  ;
our goal is to devise adaptive processes in which the parameters of all
units converge to such values that every unit becomes specifically matched
or sensitive to a particular domain of input signals in a regular order.
Instead of considering the maximum output response, the location
of the maximum may also be regarded as defining the best match between
the input vectors
;
our goal is to devise adaptive processes in which the parameters of all
units converge to such values that every unit becomes specifically matched
or sensitive to a particular domain of input signals in a regular order.
Instead of considering the maximum output response, the location
of the maximum may also be regarded as defining the best match between
the input vectors 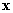 and
the weight vectors
and
the weight vectors  .
Widely applied matching criterion is the Euclidean distance between vectors.
If we define the best match to be due at unit with index
.
Widely applied matching criterion is the Euclidean distance between vectors.
If we define the best match to be due at unit with index  ,
then
,
then  can
be determined by the condition:
can
be determined by the condition:
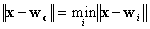 .
.
For the processing units of the array, some model law of
the basic adaptive units should be chosen. The adaptation equation may
be of the form:
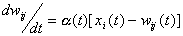 for
for  ,
,
where 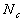 denotes a topological neighborhood which is defined such that all units
that lie within a certain radius from unit
denotes a topological neighborhood which is defined such that all units
that lie within a certain radius from unit  are
included in
are
included in 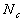 and
and 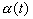 is
the gain sequence, which is usually a slowly decreasing function of time.
Now the SOM algorithm can be summarized as follows.
is
the gain sequence, which is usually a slowly decreasing function of time.
Now the SOM algorithm can be summarized as follows.
-
t=0
-
Initialize the topological neighborhood
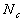 and
the gain sequence
and
the gain sequence 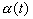 .
.
-
Repeat
 t = t +1
t = t +1
 Present a new
selected feature vector
Present a new
selected feature vector 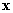 to
the algorithm
to
the algorithm
 Determine the
winning representative
Determine the
winning representative 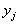 ,
according to the matching criterion
,
according to the matching criterion
 Parameter Updating
Parameter Updating
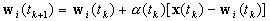 for
for  ,
,
 otherwise
otherwise
 End
End
-
Until convergence has occurred OR
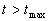
-
Identify the clusters represented by
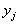 's, by assigning each vector
's, by assigning each vector 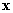 to the cluster that corresponds to the representative closest to
to the cluster that corresponds to the representative closest to 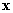 .
.
A proper choice for 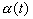 and
and 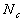 can best be determined by experience. Certain "rules of thumb" can be invented
easily after some experience. Moreover, it may be useful to notice that
there are two phases in the formation of maps that have a slightly different
nature, that is, initial formation of the correct order and final convergence
of the map into asymptotic form. For good results, the latter phase may
take 10 to 100 times as many steps as the former, whereby a low value of
can best be determined by experience. Certain "rules of thumb" can be invented
easily after some experience. Moreover, it may be useful to notice that
there are two phases in the formation of maps that have a slightly different
nature, that is, initial formation of the correct order and final convergence
of the map into asymptotic form. For good results, the latter phase may
take 10 to 100 times as many steps as the former, whereby a low value of 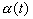 is used.
Once again, we emphasize that many experiments have indicated
the following general rules to form the basis of various self-organizing
processes:
is used.
Once again, we emphasize that many experiments have indicated
the following general rules to form the basis of various self-organizing
processes:
-
Locate the best matching unit.
-
Increase matching at this unit and its topological neighbors.
[Return to Index]
4. Dimensionality Reduction (KL Transformation)
The basic concept of dimensionality reduction is to transform
a given set of measurements to a set of features. If the transform is suitably
chosen, transform domain can exhibit high "information packing" properties
compared with the output samples. This means that most of the classification-related
information squeezed in a relatively small number of features, leading
to a reducing necessary feature space dimension.
The KL transformation is a popular method of reducing
dimensionality. Let 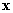 denote
the feature vector in the thyroid data. The goal of the KL transform is
to generate features that are optimally uncorrelated. Let
denote
the feature vector in the thyroid data. The goal of the KL transform is
to generate features that are optimally uncorrelated. Let
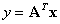 ,
,
and A is chose so that its columns are the orthonormal eigenvectors
of the correlation matrix 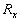 of
the feature vectors. Furthermore, if we assume the
of
the feature vectors. Furthermore, if we assume the 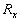 positive
definite, the eigenvalues are positive. The resulting transform is known
as the KL transform and it achieves the original goal of generating mutually
uncorrelated features.
[Return to Index]
positive
definite, the eigenvalues are positive. The resulting transform is known
as the KL transform and it achieves the original goal of generating mutually
uncorrelated features.
[Return to Index]
5. Experimental Results
In this section, we show the performance of the conventional
classifiers and SOM method. We also show the effect of the KL transform
on the classification problem. The thyroid data are used for all these
classifiers.
First, let us consider the conventional methods including
Bayes, Linear classifier and 1-NN. The total 5 features of the thyroid
data are retained. The classification errors of each method are listed
in Table 5.1:
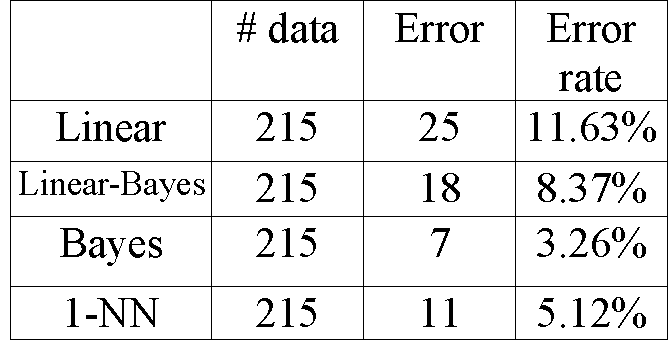
Table 5.1: Comparison of four popular classifiers.
Note that Bayes classifier gives the best result, since the
error rate of it is the lowest among the four classifiers. Also, we remark
that Bayes classifier makes a resubstitution procedure, while 1-NN uses
the leave-one-out method. So, we cannot say Bayes is better than 1-NN from
the results above. Since the error rate of linear classifier is as high
as 11.63%, the thyroid data are not linearly separated.
Then the KL transformation is applied to the thyroid data.
We only keep the first two main features from the KL results. That is,
the dimension of the data is reduced from 5 to 2. Mainly because we want
to plot the boundaries of each classifier in the 2-D space. Table 5.2 shows
the experiment results of the same four classifiers after KL transform.
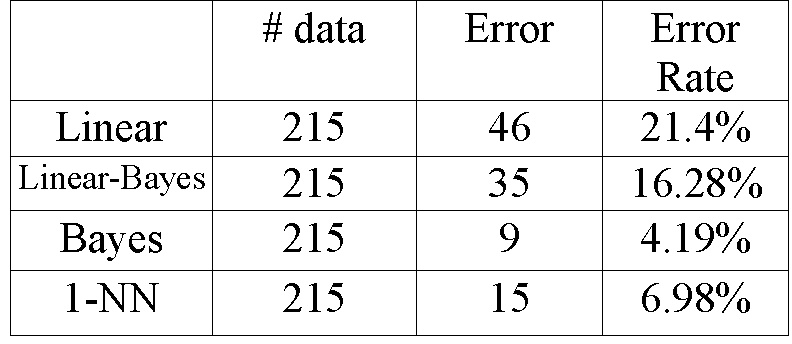
Table 5.2: Comparison of four classifiers after KL transform.
We note that Bayes again outperforms all other classifiers.
But the error rates of each method are higher than those before KL transform.
The reason is that some important features of the thyroid data are lost
in the procedure of KL transform. As mentioned previously, after KL transform,
we can show the decision boundaries of all the classifiers. We show the
boundaries of linear classifier, Bayes and linear-Bayes methods in the
2-D case in the Figure 5.1, 5.2, and 5.3, respectively.
Figure 5.1: Decision Boundaries of Linear Classifier.
(Click here: Figure 5.1 )
Figure 5.2: Decision Boundaries of Linear-Bayes Classifier.
(Click here: Figure 5.2 )
Figure 5.3: Decision Boundaries of Bayes Classifier. (Click
here: Figure 5.3 )
From these figures, we explicitly know how each conventional
classifier works.
Now, let us consider the SOM neural network. We first take
half of the data as the training data, and the remains as the testing data.
Then we make a resubstitution test, that is, all the data are used to train
the SOM, and then use them again to test the SOM. The gain sequence in
the SOM is chosen as 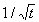 ,
and the maximum number of iteration is 10000. We give the results of such
two tests in the Table 5.3.
,
and the maximum number of iteration is 10000. We give the results of such
two tests in the Table 5.3.
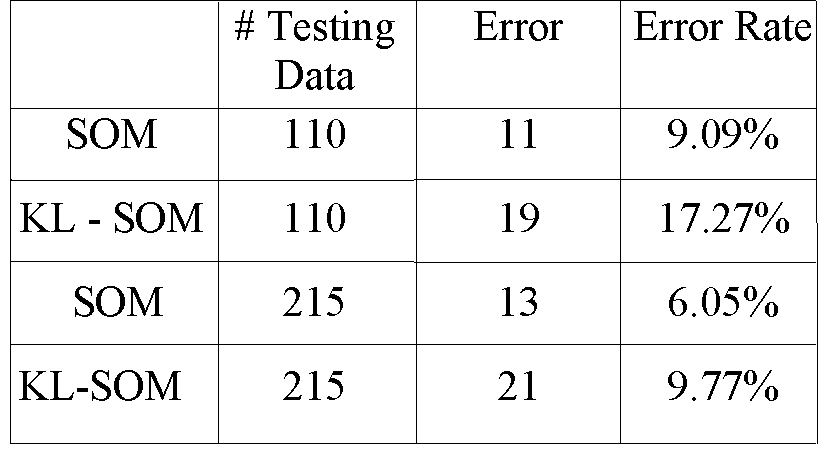
Table 5.3: The Error Rates of SOM.
Compare the results in Table 5.1, 5.2, and 5.3, we note that
the performance of the SOM is not better than that of Bayes and 1-NN methods,
it is only better than the linear classifier. The main reason is that the
training data are not sufficient. In the thyroid database, there are only
35 vectors for the class of hyperthyroid function and 30 vectors for the
hypothyroid function. Another reason is that the relative quantities of
three classes data are not similar. 150 vectors are for the normal functional
data, which is 5 times as many as the other two classes. To show how the
SOM works explicitly, we give a map of the 2-D representations in the Figure
below.
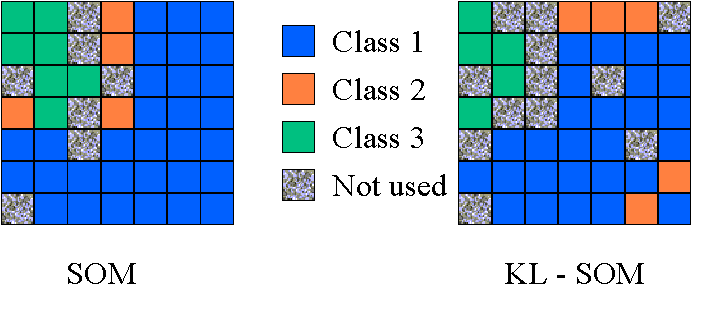 We make the representations as a 7-by-7 array. Each square
block denotes one output of the SOM system. After the training, we see
that the data of each class cluster to a different region in the 2-D representations.
When testing, if the data from one class is mapped into the corresponding
regions in the 2-D space, then the classification of the data is right.
Otherwise, it is an error. Also note that the 2-D representation after
KL transform is a little bit intercrossed, because two blocks representing
the class 2 are located in the region of the class 1. That is the reason
why the error rate of KL-SOM is higher than that of SOM.
[Return to Index]
We make the representations as a 7-by-7 array. Each square
block denotes one output of the SOM system. After the training, we see
that the data of each class cluster to a different region in the 2-D representations.
When testing, if the data from one class is mapped into the corresponding
regions in the 2-D space, then the classification of the data is right.
Otherwise, it is an error. Also note that the 2-D representation after
KL transform is a little bit intercrossed, because two blocks representing
the class 2 are located in the region of the class 1. That is the reason
why the error rate of KL-SOM is higher than that of SOM.
[Return to Index]
6. Conclusions
We have shown that Bayes classifier with resubstitution procedure
gives the best classification results in this problem. It has been shown
that KL transform makes the classification worse for all kinds of classifiers
in this three-class case. SOM is a promising method for pattern recognition.
Although it is not the best classifier in the problem, we have shown that
the more the number of training data, the better the performance of the
SOM.
[Return to Index]
7. Appendix
We have the MATLAB codes for all the classifiers discussed
above, including the Self-Organizing Mapping. If you have any questions
about this report or if you are interested in our MATLAB codes, please
feel free to contact us at:
 kun@dsp.ufl.edu
kun@dsp.ufl.edu
Reference:
[1] D. Coomans and I. Broeckaert, "Potential Pattern Recognition
in Chemical and Medical Decision Making," Research Studies Press, 1986.
[2] D. Coomans, I. Broeckaert, M. Jonckheer and D.L. Massart,
"Comparison of Multivariate Discrimination Techniques for Clinical data
– Application to the thyroid Functional State," Methods of Information
in Medicine, Vol. 22, pp. 93-101, 1983.
[3] Teuvo Kohonen, "Self-Organization and Associative
Memory," Springer-Verlag Berlin Heidelberg New York, 1989.
[4] Cornelius T. Leondes, "Algorithms and Architectures,"
Academic Press, 1998.
[5] Sergios theodoidis and konstantinos Koutroumbas, "Pattern
Recoginition," Academic Press, 1998.
[Return to Index]
![]() ,
, ![]() ,
and
,
and ![]() denote
the class of normal thyroid function, hyper-thyroid function, and hyperthyroid
function, respectively. An unknown pattern in each class is represented
by a feature vector
denote
the class of normal thyroid function, hyper-thyroid function, and hyperthyroid
function, respectively. An unknown pattern in each class is represented
by a feature vector ![]() ,
where
,
where ![]() . First,
conventional classifiers are applied to the data without dimensionality
reduction, including Bayes method, Linear classifiers, and 1-NN. A kind
of neural network, Kohonen Self-Organizing Mapping (SOM) [3, 4], is also
used to the original data. Second, we use KL transformation to reduce the
dimension of the sampled data, then input the transformed data to the four
classifiers used previously, including the SOM neural network. In this
problem, since some information is lost after KL transform, the misclassification
rates increase in the low dimension case.
. First,
conventional classifiers are applied to the data without dimensionality
reduction, including Bayes method, Linear classifiers, and 1-NN. A kind
of neural network, Kohonen Self-Organizing Mapping (SOM) [3, 4], is also
used to the original data. Second, we use KL transformation to reduce the
dimension of the sampled data, then input the transformed data to the four
classifiers used previously, including the SOM neural network. In this
problem, since some information is lost after KL transform, the misclassification
rates increase in the low dimension case.
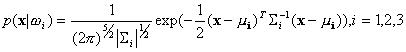 ,
,



